Modeling the Supplier as a Queueing System
In most inventory models it is assumed that the supplier who delivers the replenishment orders has unlimited capacity. If his capacity is limited, then this is only reflected by the replenishment lead time (= waiting time of customer orders at the supplier) which then is no longer deterministic but is considered as an external random variable.
In the sequel we will go further into the question as to how the logistical performance of a delivery node in a supply network is affected by limited capacities, and how this influences the safety inventory that must be held at a delivered customer node. In the discussion it is to be differentiated between delivery nodes that produce to stock and delivery nodes that start production only after a customer order has already arrived, according to the make-to-order principle. In case of make-to-stock production, the minimal inventory-related customer waiting time is zero which happens when an arriving customer order finds positive inventory on hand. In case of make-to-order production, theminimum waiting time equals the minimum flow time of the associated production order which is the sum of the processing time and the queueing time the production order spends in the production system.
Make-to-Order production
With make-to-order production the supplier is a production node which starts producing only after the customer order has arrived. This behavior can be represented with the help of a queueing model. Queueing theory provides a wide variety of exact and approximate models that enable us to compute the performance indicators of interest for many different real-life situations.
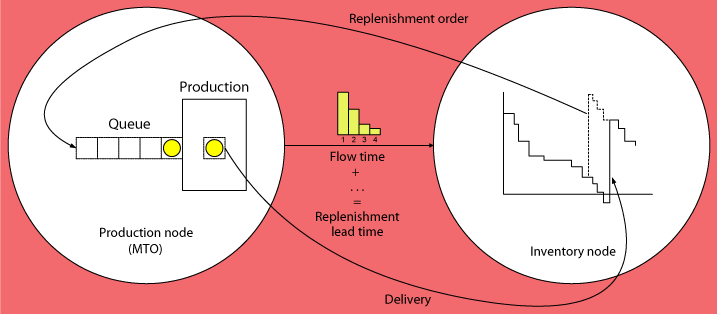
The following Figure illustrates the structure of the two-stage supply chain that results if we include the characteristics of the supplying node into the scope of the inventory model used at the customer node. The inventory node sends a replenishment order to the supplier (the production node) who generates a production order and sends this to the production stage. After completion of production the goods are delivered to the customer node. The replenishment lead time seen by the customer node is equal to the sum of the waiting time of the production order before the start of processing, the processing time, and the time required for handling and shipping, which may include additional waiting times. The length of this replenishment lead time plays an important role in the determination of the safety inventory required at the customer node.
Continuous time axis
We assume first that in the inventory node a base-stock policy with Poisson distributed demand arriving on a continuous times axis is in effect. In this case, the order arrival process at the inventory node is identical to the order arrival process at the production stage. If, in addition, the processing times are exponentially distributed, the production node can be modeled as an $M/M/1$ queueing system. The flow time in this system is exponentially distributed with the parameter $(\mu-\lambda)$ which is the difference of the processing rate $\mu$ and the arrival rate $\lambda$. Neglecting the handling and transportation time between production and inventory, the replenishment lead time is equal to the flow time in the production node and, therefore, also exponentially distributed with the parameter $(\mu-\lambda)$. As, according to the above assumption, the customer arrivals are Poisson distributed, the demand during the replenishment lead time of the inventory node follows a geometric distribution with the parameter $p=\frac{(\mu-\lambda)}{\lambda+ (\mu-\lambda)} = (1-\frac{\lambda}{\mu})$, which starts from 0:
$P\{Y=n\}=(1-p)^{n}\cdot p= \left(\frac{\lambda}{\mu}\right)^n\cdot \left(1-\frac{\lambda}{\mu}\right) \qquad n=0,1,2,\ldots$
For an example with the arrival rate $\lambda=2.5$ and the processing rate $\mu=3$, the following Table shows the relation between the order level $S$ and the expected backlog as well as the $\beta$ service level for a demand during the replenishment lead time which is geometrically distributed with the parameter $p=\frac{3-2.5}{3}=0.1667$. With an average replenishment lead time of $\frac{1}{3-2.5}=2$ periods, the expected lead time demand is $E\{Y\}=2\cdot 2.5 = 5$.
| $S$ | $E\{I^f\}$ | $\beta$ |
| 4 | 2.4113 | 0.5177 |
| 6 | 1.6745 | 0.6651 |
| 8 | 1.1628 | 0.7674 |
| 10 | 0.8075 | 0.8385 |
| 12 | 0.5608 | 0.8878 |
| 14 | 0.3894 | 0.9221 |
Discrete time axis
The results for a discrete time axis are available in the book. Further topics:
Make-to-Stock production
Production nodes with unlimited capacity
Production nodes with limited capacity